Python : statistics and simple models

Work in progress

This page aims to have an overview of basic knowledge about data analysis and how we should apprehend a dataset. Which tools can we use to have a better insight of our data?

1. Data

quantitative data : variables which are made of numerical values. Values could be continuous or discrete.

Ex1 : temperature is a continuous quantitative variable

Python
1
2
3
temperatures=[20,18.7,-3.4,32,0,3,-10.8]
>>>temperatures
[20,18.7,-3.4,32,0,3,-10.8]

Ex2 : number of kids in a family is a discrete quantitative variable

Python
1
2
3
kids_qty=[2,0,4,1,1,0,3]
>>>kids_qty
[2,0,4,1,1,0,3]

qualitative data : they represent categories. Labeling can be done using text or numerical values. A qualitative variable can be ordinal or nominal. We say it’s an ordinal variable if ordering these values have a meaning.

Ex3 : locations (eg countries) are nominal qualitative values

Python
1
2
3
locations=["USA","France","Thailand","Argentina","France","France","USA"]
>>>locations
["USA","France","Thailand","Argentina","France","France","USA"]

Ex4 : segment of a market can be ordinal values

Python
1
2
3
market_value_segment=["big","small","medium","big","medium","medium","small"]
>>>market_value_segment
["big","small","medium","big","medium","medium","small"]

dates, times

different format can be found in dataset. Here is a description of some usual format and some tools to manipulate it in python.

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import time
import datetime
import pandas as pd
 
#time
timestamp=time.time() #unix epoch : number of second since 1st January 1970 at 00:00:00
time.localtime()
 
#datetime
now=datetime.datetime.now()
print(now.year)
print(now.month)
print(now.day)
print(now.hour)
print(now.minute)
print(now.second)
print(now.isoformat())
 
#pandas time range and timestamp operation
timerange=pd. date_range('6-21-2018',periods=20,freq='D')
timerange #time range have frequencies
#DatetimeIndex(['2018-06-21', '2018-06-22', '2018-06-23', '2018-06-24',
#              '2018-06-25', '2018-06-26', '2018-06-27', '2018-06-28',
#               '2018-06-29', '2018-06-30', '2018-07-01', '2018-07-02',
#               '2018-07-03', '2018-07-04', '2018-07-05', '2018-07-06',
#               '2018-07-07', '2018-07-08', '2018-07-09', '2018-07-10'],
#              dtype='datetime64[ns]', freq='D')
 
timestamp=pd.Timestamp('2-23-2019 14:17:45.5')
 
timedelta=pd.Timedelta('1 day')
 
timeperiod=pd.Period('2-23-2019')
timeperiod.start_time
timeperiod.end_time
 
#converting to period and timestamp
ts_dt.to_period()
ts_pd.to_timestamp()
 
#formating date
 
#working with time zones
from pytz import common_timezones,all_timezones
t=timestamp.tz_localize(tz='US/Central')
t=t.tz_convert('utc') #convert everything to utc time
 
#read datetime properly with read_fwf

Nothing fancy here, we just need to remember that several format for time can be found in dataset and that we shall have to translate everything to the same format for further analysis. Pandas library has great tool to test if a particular timestamp belongs to a period of time.

pictures (as bitmap arrays)

Pictures are arrays of pixels. In a grey scaled image, each pixel can be represented by a value between 0 (white) and 255 (black).

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#load colored picture in a dataframe
import numpy as np
from PIL import Image
image=Image.read('forest.jpg')
image=np.asarray(image) #transform image in a numpy array
image
 
#array([[[123, 124,  30],
#        [124, 139,   0],
#        [126, 140,   1],
#        ...,
#        [ 89,  77,  25],
#        [ 83,  71,  21],
#        [ 87,  69,  29]],
# .......
 
#we can check the shape of our array
image.shape
#returns (429,640,3)

 

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#load grey scaled picture in a dataframe
image=Image.read('forest.jpg')
image=np.asarray(image)
image
 
#array([[118, 125, 128, ...,  76,  70,  71],
#       [ 79, 106, 115, ...,  74,  69,  63],
#       [ 46,  78,  93, ...,  88,  88,  77],
#       ...,
#       [104, 107,  86, ..., 132, 139, 123],
#       [117, 121, 113, ..., 138, 138, 132],
#       [101,  94,  94, ...,  97,  91,  96]], dtype=uint8)
 
#check shape of our array
image.shape
#returns (429,640)

sounds (.wav format)

original map3 piano file : https://www.auboutdufil.com/get.php?web=https://archive.org/download/auboutdufil-archives/492/Myuu-TenderRemains.mp3

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from scipy.io import wavefile
fs, data=wavfile.read('piano.wav')
fs
#44100
data
#array([[0, 0],
# [0, 0],
# [0, 0],
# ...,
# [0, 0],
# [0, 0],
# [0, 0]], dtype=int16)
data.shape
#(13100119,2)
# 13100119 / 44100 = 297 s (which is the duration of our sound file)

Python
1
2
3
#sample of data
sample=data[0:100000,:]
plt.plot(sample)

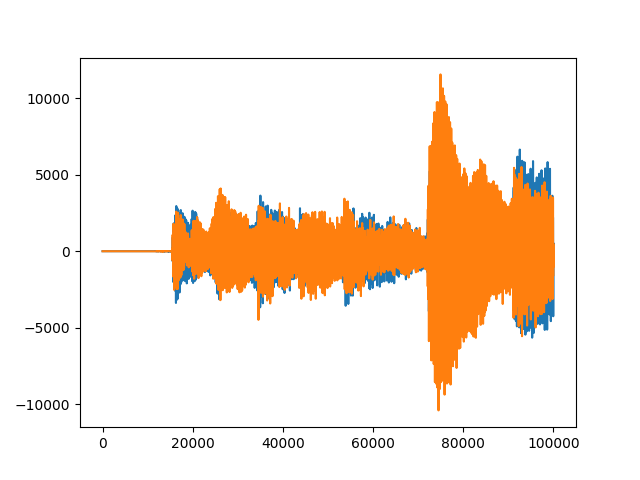
We can visualize the 2 channels (orange and blue) of the audio file. The discrete time is \frac {1}{fs} second.

2. Distributions

For this study let’s group the variables we created in chapter 1 into a single pandas dataframe. All our lists contains the same amount of elements.

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd
import numpy as np
 
data=pd.DataFrame(np.column_stack([temperatures,locations,kids_qty,market_value_segment]),columns=["temperature","locations","kids_qty","market_value"])
>>>data
temperature  locations kids_qty market_value
0        20.0        USA        2          big
1        18.7     France        0        small
2        -3.4     France        4       medium
3        32.0  Argentina        1          big
4         0.0     France        1       medium
5         3.0        USA        0       medium
6       -10.8   Thailand        3        small

Python
1
2
data.shape
(7,4)

data.shape returns the size of our data set, we have 7 individuals represented by 4 different features.

For each feature, let’s try to represent its distribution graphically.

a. Pie chart (qualitative data) : on locations column

Python
1
2
3
4
5
6
7
import matplotlib.pyplot as plt
#count the occurence for each label in locations
location_count=data["locations"].value_counts()
#plot associated piechart
location_count.plot(kind='pie')
plt.axis('equal')
plt.show()

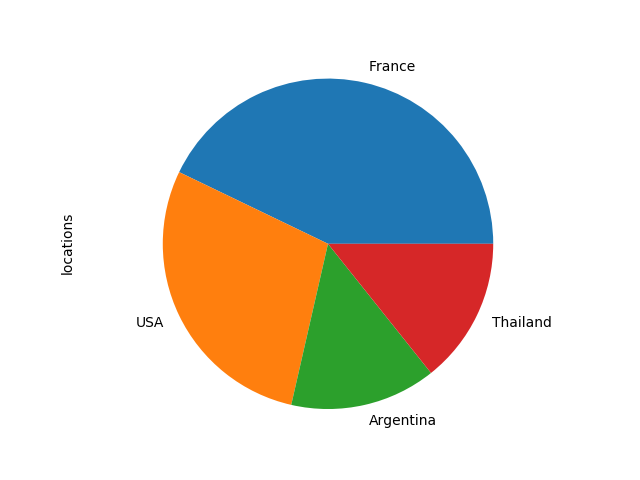
We can access the labels and values of our counts array using these commands :

Python
1
2
3
4
5
6
7
location_count.index
#returns
#Index(['France', 'USA', 'Argentina', 'Thailand'], dtype='object')
 
location_count.values
#returns
#array([3, 2, 1, 1])

 

b. barchart (qualitative data) : on market_value column

Python
1
2
3
4
5
#count occurences
market_count=data["market_value"].value_counts()
#plot it!
market_count.plot(kind='bar')
plt.show()

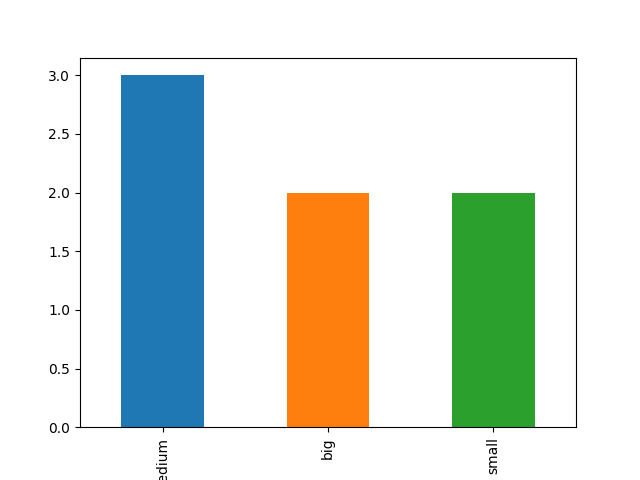
c. histogram (quantitative data) :

loading a bigger dataset for this chart (iris dataset see 6. Correlation)

Python
1
2
3
#plot it!
iris["sepal_length"].hist()
plt.show()

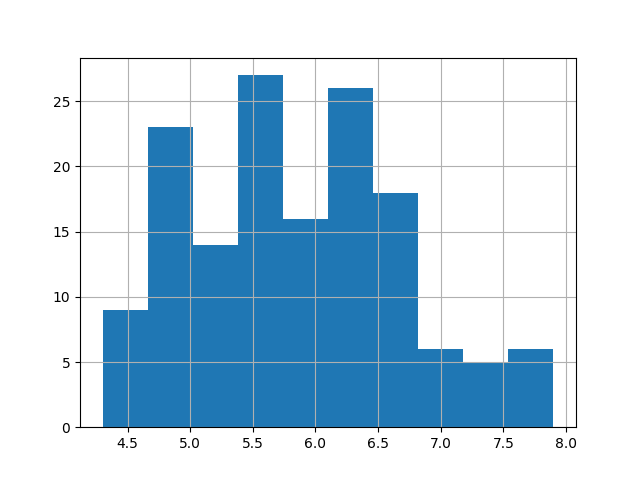
d. densities plot

Python
1
2
import seaborn as sns
sns.kdeplot(iris["sepal_length"],shade=True)

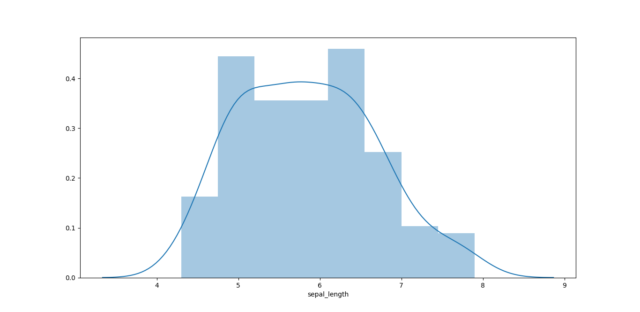
3. Statistical inference

Statistical inference is the process of making conclusion about populations from data. One way to draw conclusion about a population is to observe a sample of it. We are using indicators to describe a variable (they are called estimators). Still, one has to be aware that summing up data with estimators must be done with care and that we should keep an eye on the distribution of our values. An estimator is said to be relevant if :

  • it is consistant
  • it has low bias and low variance

let’s review the most common estimators used in statistics.

a. mode

In a list, mode is the most represented value.

Python
1
2
3
4
from statistics import mode
mode(locations)
#returns
#'France'

b. mean

mean a a variable is defined by :

\bar{x}=\frac{\sum x}{n}

 

Python
1
2
3
np.mean(temperatures)
#returns
#8.500000000000002

c. median

median is the value that divide your variable in 2 groups with equal amount of individuals.

Python
1
2
3
np.median(temperatures)
#returns
#3.0

d.variance and standard deviation

\sigma=\sqrt{\frac{\sum (x-\bar{x}) ^{2}}{n-1}}

 

standard and variance are a measurement of dispersion.

Python
1
2
3
4
5
6
7
8
9
#Variance
np.var(temperatures)
#returns
#200.73428571428576
 
#Standard deviation
np.std(temperatures)
#returns
#14.168072759351773

e. quantile, interquartile, decile, etc…

Q1 : value that cut the dataset with 1/4 of individuals under Q1 and 3/4 above Q1

Q3 : value that cut the dataset with 3/4 of individuals under Q3 and 1/4 above Q3

IQ interquartile distance : IQ = Q3 – Q1

Python
1
2
3
4
5
6
7
8
9
10
11
12
#Q1
Q1=iris["sepal_length"].quantile(q=0.25)
print(Q1)
#5.1
#Q3
Q3=iris["sepal_length"].quantile(q=0.75)
print(Q3)
#6.4
#IQ
IQ=Q3-Q1
print(IQ)
#1.3

IQ is often use to remove outliers from our dataset (see outliers and missing values part).

f. range

Is the range of your variable. Difference between the minimum and the maximum value in your variable.

Python
1
2
3
np.ptp(temperatures)
#returns
#42.8

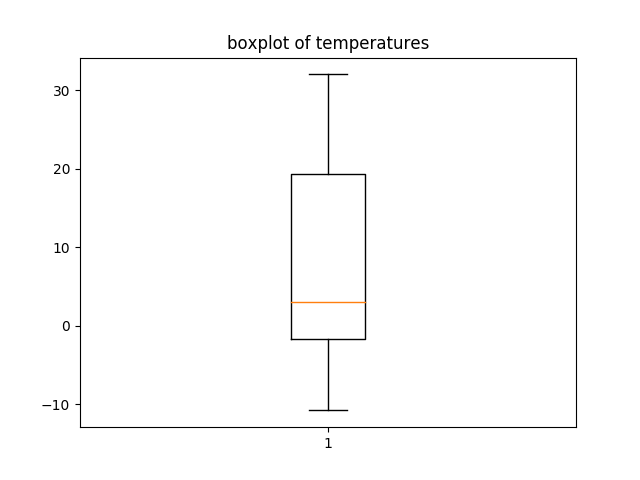
g. boxplot

A good representation a dataset and some of its statistics is the boxplot. On this chart we can read values associated to quantiles : median, Q1,Q3, Q1-1.5IQ, Q3+1.5IQ. Outliers are plotted as dots.

Python
1
2
3
plt.boxplot(temperatures)
plt.title('boxplot of temperature')
plt.show()

4. Skewness

Skewness is a measurement of symmetry (comparison of mode and mean).

Python
1
2
3
4
#calculation of skewness
skewness=data["temperature"].skew()
#returns
#0.384469564140117

3 cases :

skewness=0 : the distribution is symmetric

skewness<0 : the distribution is spreading more on the left of the mean value

skewness>0 : the distribution is spreading more on the right of the mean value

5. Kurtosis

Is a measurement of flatness of our distribution.

Python
1
2
3
kurtosis=data["temperature"].kurtosis()
#returns
#-1.160628269697897

kurtosis is negative and low, which could represent quite a flat profile for our variable.

6. Correlations : bivariate analysis on quantitative variables

Correlation between 2 variable is a measure of how linearly dependent these 2 variables are. Iris data set is a famous dataset use in data science in order to understand the basic principles. I’ll use it to illustrate the correlation.

r(x,y)=\frac{1}{n-1}\sum \frac{(x-\bar{x})(y-\bar{y})}{\sigma_{x}\sigma_{y}}

 

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#library to plot heatmap
import seaborn as sns
 
iris=pd.read_csv("iris.data",header=None)
# first 4 columns are numerical values representing measurement on flower. The last columns is a label with type of flower (3 differents class)
#naming columns
iris.columns=["sepal_length","sepal_width","petal_length","petal_width","class"]
#print head
iris.head()
   sepal_length  sepal_width  petal_length  petal_width        class
0           5.1          3.5           1.4          0.2  Iris-setosa
1           4.9          3.0           1.4          0.2  Iris-setosa
2           4.7          3.2           1.3          0.2  Iris-setosa
3           4.6          3.1           1.5          0.2  Iris-setosa
4           5.0          3.6           1.4          0.2  Iris-setosa
#select first 4 columns
X=iris.iloc[:,0:4]
# let's calculate correlations on our measurements (using pandas correlation function)
correlation=X.corr()
#plotting correlation
sns.heatmap(correlation)
plt.show()

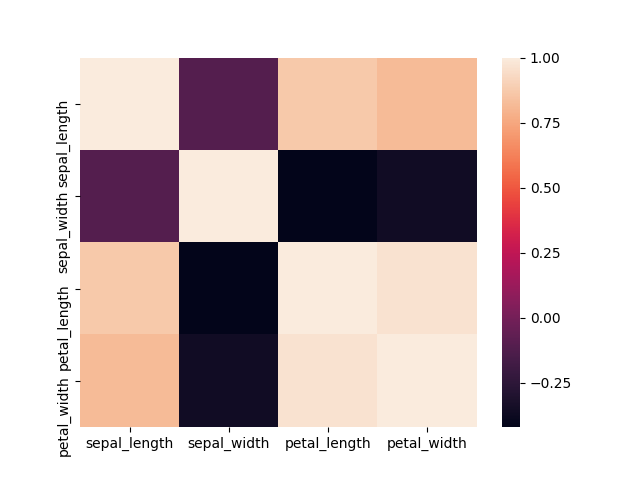
1
2
3
4
5
6
7
print(correlation)
#returns
#                sepal_length  sepal_width  petal_length  petal_width
#sepal_length      1.000000    -0.109369      0.871754     0.817954
#sepal_width      -0.109369     1.000000     -0.420516    -0.356544
#petal_length      0.871754    -0.420516      1.000000     0.962757
#petal_width       0.817954    -0.356544      0.962757     1.000000

Interpretation : Positive values of correlation indicates that variables tend to evolve in the same way (when one is growing, the other one do the same), whereas negative value of correlation indicates that variables tend to evolve differently (one one is growing the other one tend to decrease).

Too much linearly correlated variables shall not be used at the same time for modeling. Removing one of the variable or creating a new feature from this variables is a good idea to address this problem.

7. Scatter plot

Plotting relation between 2 quantitative variables:

Python
1
2
3
4
plt.scatter(iris["petal_length"],iris["petal_width"])
plt.xlabel('iris["petal_length"]')
plt.ylabel('iris["petal_width"]')
plt.show()

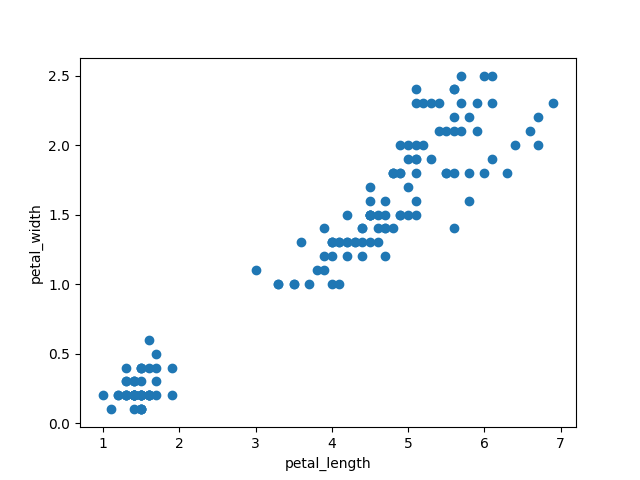
labeling data with colors

Python
1
2
3
colors={'Iris-setosa':'red','Iris-versicolor':'green','Iris-virginica':'blue'}
plt.scatter(iris["petal_length"],iris["petal_width"],c=label.apply(lambda x:colors[x]))
plt.show()

Python
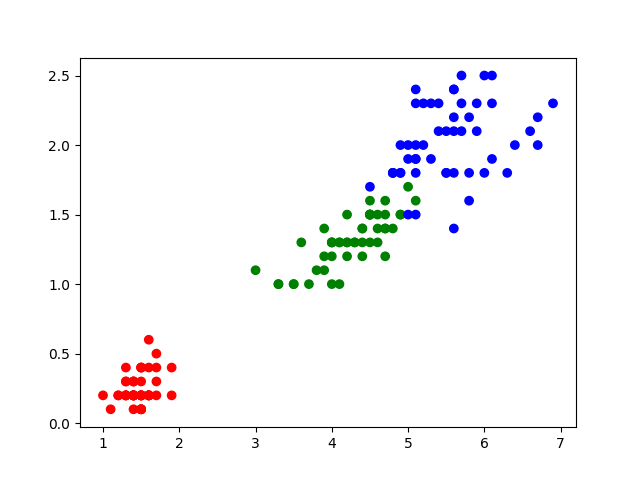
1
2
3
#plotting scatter plot
pd.plotting.scatter_matrix(measurements)
plt.show()

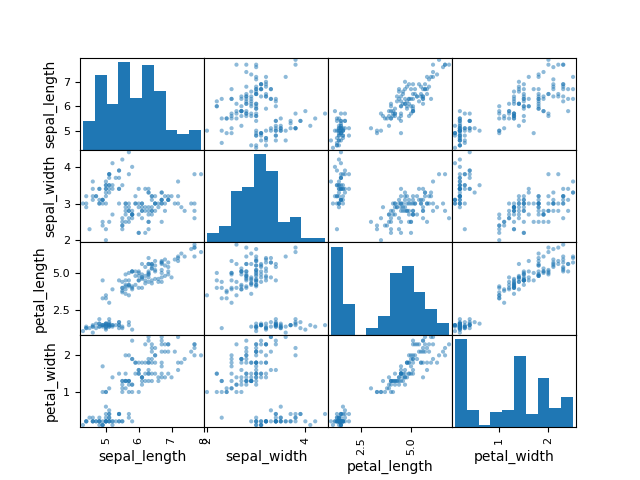
it is a good way to assess any tendencies between 2 variables and to check the distributions of each variables from our dataset.

8. ANOVA : bivariate analysis on mixed variables

let’s try to analyze our iris dataset and compare sepal_length per class of flower.

Python
1
iris.boxplot(column="sepal_length",by="class")

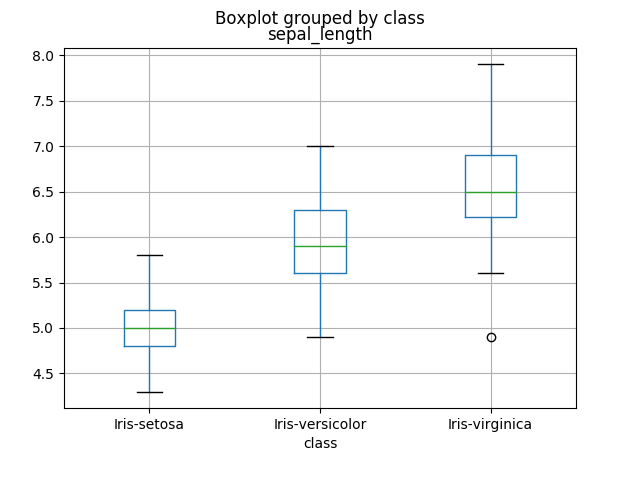
How can we evaluate a correlation between a qualitative and a quantitative variable?

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def eta_squared(x,y):
    moyenne_y = y.mean()
    classes = []
    for classe in x.unique():
        yi_classe = y[x==classe]
        classes.append({'ni': len(yi_classe),
                        'moyenne_classe': yi_classe.mean()})
    SCT = sum([(yj-moyenne_y)**2 for yj in y])
    SCE = sum([c['ni']*(c['moyenne_classe']-moyenne_y)**2 for c in classes])
    return SCE/SCT
 
eta_squared(iris["class"],iris["sepal_length"]
#returns
#0.6187057307384859

 

9. Chi-2 test

Chi-2 test checks if whether or not 2 variables are related or not. We have the following hypothesis.

H0 : the 2 variables are independent

H1 : the 2 variables are not independent

 

10. Outliers and missing values

Dataset are not always perfect and frequently presents missing values and inconsistent data.

count missing values

Python
1
2
df.isnull().sum
#return qty of missing values in the dataframe

If missing values can be found in only a small amount of individual in our dataset, we could simply drop this individuals.

Python
1
df.dropna()

remove outliers using quartiles

Outliers is value that appears to be far away and unusual in a given variable or set of individuals. One has to detect and remove them before trying to build a model from data. Their influence is also bad for our statistical estimations. Outliers can be found in a variable, but some individual in our dataset can also be considered as outliers. Before considering any statistical analysis or modeling, we should clean our data from these values.

We usually use our InterQuantile distance to detect outliers

Python
1
2
3
4
5
6
7
8
#calculate Q1
q1=data['var'].quantile(0.1)
 
#calculate Q3
q3=data['var'].quantile(0.9)
 
#filter out outliers
data=data[(data['var']>q1)&(data['var']<q3)]

missing values imputation

imputing mean or median of the sample is an easy strategy and will have bad impact on modelling

A slightly better approach is to build a simple model with the use of other variables.

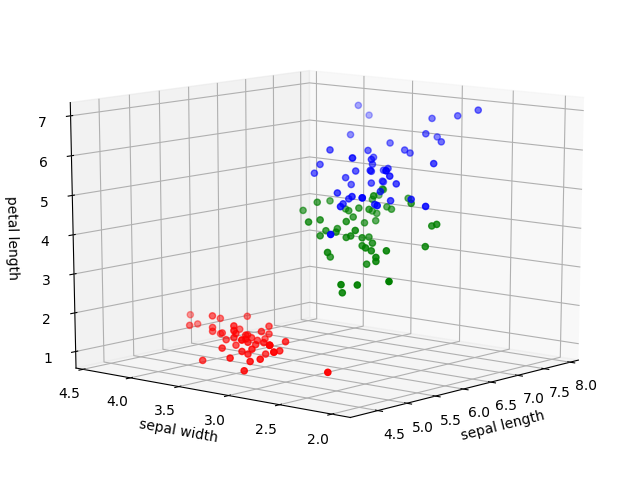
11. 3d scatterplot

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from mpl_toolkits.mplot3d import Axes3D
x=iris["sepal_length"]
y=iris["sepal_width"]
z=iris["petal_length"]
label=iris["class"]
 
 
#transform label into colors
label.unique()
#array(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'], dtype=object)
colors={'Iris-setosa':'red','Iris-versicolor':'green','Iris-virginica':'blue'}
c=label.apply(lambda x:colors[x])
 
 
fig=plt.figure()
ax=Axes3D(fig)
ax.scatter(x,y,z,c=c)
 
ax.set_xlabel('sepal length')
ax.set_ylabel('sepal width')
ax.set_zlabel('petal length')
 
plt.show()

12. Dimensionality reduction

Reduction of the number of features in our dataset is a good option to reduce our computation time when building our model. Nevertheless, we are loosing some information when reducing the space and it should always be made carefully.

a. PCA

Python
1
2
from sklearn.decomposition import PCA
#reducing iris dataset from 4 to 2 dimensions

disadvantage of PCA : we are loosing the readability of our features (because our data is projected in a brand new space).

b. features selection

13. basic signal processing

see more about time series and signal processing on this page.

autocorrelation

Python
1
2
3
4
def autocorrelate(x):
norm=np.sum(x**2)
c=np.correlate(x,x,mode='full')/norm
return c

autocorrelation of a signal helps to find periodicities in a signal.

temporal to frequency : Fast Fourier Transformation

Python
1
2
3
4
5
#selecting 1 channel of our wav array
channel=sample[:,0]
T=len(data)/fs
fft=fft(channel)
frq=np.arange(len(data))/

14. Normalizations

Variables in a dataset usually runs on very different range. Normalizations techniques helps to bring every variable to a same range : usually [0,1] or [-1,1]. I’ll introduce the 2 most easy to use and famous type. Please refer to this wikipedia page for more information.

a. standard core

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn import preprocessing
 
X_norm=preprocessing.normalize(measurements)
X_norm=pd.DataFrame(X_norm)
X_norm.head()
 
#results
#          0         1         2         3
#0  0.803773  0.551609  0.220644  0.031521
#1  0.828133  0.507020  0.236609  0.033801
#2  0.805333  0.548312  0.222752  0.034269
#3  0.800030  0.539151  0.260879  0.034784
#4  0.790965  0.569495  0.221470  0.031639

b. feature scaling

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn import preprocessing
 
X_scale=preprocessing.scale(measurements)
X_scale=pd.DataFrame(X_scale)
X_scale.head()
 
#results
#     0         1         2         3
#0 -0.900681  1.032057 -1.341272 -1.312977
#1 -1.143017 -0.124958 -1.341272 -1.312977
#2 -1.385353  0.337848 -1.398138 -1.312977
#3 -1.506521  0.106445 -1.284407 -1.312977
#4 -1.021849  1.263460 -1.341272 -1.312977

15. Probabilistic distribution models

There are a lot of different models to simulate the behavior of a variable. In the following, I am just going to describe the mostly used. Please refer to this wikipedia page for more insight.

Normal law : a random variable X follows a normal law, we write X~N(µ,/sigma^{2}). This law is often used to model natural phenomenon. Practically, it’s very common to meet this kind of variable in our datasets.

Bernoulli :

Bernoulli law allows to calculate the probability distribution of a random variable taking the value 1 with probabilty p and 0 with probability q=1-p.

Repeating the experience n times, we want to calculate the probability that

Poisson :

Chi2 : let’s assume a random variable X follows a normal law

We create a new variable Q, such as Q=X^{2}, we say that Q follows a Chi2 law Q~Chi^{2} with 1 degree of freedom

We can invent a new variable Q_{2}= X_{1}^2+X_{2}^2 ~Chi2 with 2 degrees of freedom

 

16. Statistic inference : the frequentist and the Bayesian approachs

H0 and H1

H0 is called null hypothesis

H1 is called alternative hypothesis

Significance levels (alpha, beta, type 1 and 2 errors) and p-value

17. Prestudy : run simple machine learning models

Naives and simple models (classification and regression) can be built to replace missing data with predictions values. In some cases, simple models turns out to have very good performance and we won’t really need to pursue our way to much more costly  models (in computation an time) such as neural networks.

KNN : K nearest neighbors (classification)

For a better understanding on how this classification algorithm work, please refer to this page. Knn allows to classify an individual regarding his neighbors assuming that individuals with equivalent features belong to the same group. We are choosing the K nearest neighbors of our new individual and associate it to the most common class.

Back to the example of iris flower. Here is the code to implement such a model using scikit-learn library :

Python
1
2
3
4
5
6
7
8
9
from sklearn import preprocessing,model_selection,neighbors
X=preprocessing.normalize(measurements)
y=iris["class"]
X_train,X_test,y_train,y_test=model_selection.train_test_split(X,y,test_size=0.3)
classifier=neighbors.KNeighborsClassifier()
classifier.fit(X_train,y_train)
accuracy=classifier.score(X_test,y_test)
print(accuracy)
#100%

Knn model works really good on this example. Sometimes a simple model can solve our classification task.

Knn algorithms use a lot of computation time when the number of compared features or examples in the dataset is big. We will usually avoid it when this quantities are too big (>1000) and choose an algorithm with better performance.

Linear Regression and R square coefficient of determination (value prediction)

Let’s assume that the sepal length can be approximate by a linear function of sepal_width, petal_length and petal width variable. Let’s model a simple linear model and evaluate its performance.

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn import linear_model,model_selection
y=iris["sepal_length"]
X=iris.iloc[:,1:4]
X_train,X_test, y_train,y_test=model_selection.train_test_split(X,y,test_size=0.3)
model=linear_model.LinearRegression()
model.fit(X_train,y_train)
 
#Return the coefficient of determination
model.score(X_test,y_test)
#0.7842461949239874
 
#make new prediction
model.predict(np.array([3,2,1]).reshape(1,-1))

Interpretation of R square : R square is between 0 and 1. 0 being the case where the model explain none of the variability of the data around his mean. 1 being the case where the model explains all the variability of the data around his mean. Usually of high value of R square indicates a good model. Nevertheless, this is not a sufficient condition to conclude it with certainty.

Logistic Regression (classification)

Python
1
2
3
4
5
6
7
from sklearn import linear_model
classifier=linear_model.logisticRegression()
classifier.fit(X_train,y_train)
classifier.score(X_test,y_test)
 
#returns
#86.6% of accuracy

Logistic regression has poor performance regarding this dataset.

Random Forest and Gini function (classification)

Python
1
2
3
4
5
6
7
8
from sklearn.ensemble import RandomForestClassifier
classifier=RandomForestClassifier(n_estimators=10)
classifier.fit(X_train,y_train)
accuracy=classifier.score(X_test,y_test)
print(accuracy)
 
#results
#95.5 % of accuracy

For this case Random Forest Classifier has a slightly lower accuracy than Knn. It’s often a good idea to use different models and compare their performances.

18. feature engineering

to be continued…