Time series

 

Dataset for this study : UCI

Datasets is composed of different clients (columns) for which a measurement of electric consumption has been recorded every 15 min for years. I expect to witness seasonality and trend in the signal. I’ll try to figure it out and build a regression model on it. This article aim to be an introduction to data analysis of time series.

Loading data and dependencies

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
from autocorrelation import autocorrelate
from scipy.fftpack import fft
from scipy import signal
 
#load data
data=pd.read_csv('LD2011_2014.txt',sep=";")
print(data.shape)
 
#first column is the timestamp
#every other column represent a customer
 
#convert data to proper types
data.iloc[:,0]=pd.to_datetime(data.iloc[:,0])
data.iloc[:,1]=pd.to_numeric(data.iloc[:,1].str.replace(',','.'))
 
 
#client1 prestudy
client1=data.iloc[:,0:2]
client1.columns=['timestamp','consumption']
client1.head()

Time series

Time series data are a particular form of signal type data. Usually, time series consists of a sequence of measurements. In most simple cases, every data point is recorded on a regular time basis, but usually we will be facing non regular sequences dataset. Here are 2 examples of regular and irregular time series :

  • A thermometer sensor is linked to a computer, the computer records the temperature every hour.
  • A sportsman is using a sportapp, which can record its activities.

a. Scalar product on time series : signal decomposition

Each basis must be composed with unitary vectors, and each vector must be orthogonal. We can verify these properties with the computation of the magnitude of each vector (norm of vector = 1) and the two by two scalar product of each vector in the basis.

b. Dimension of a signal

Dimension of a signal is the quantity of parameters that have an effect on the signal.

c. Mean value

mean(signal)=\frac{1}{N}\sum_{t=1}^{N}signal(t)

 

Python
1
mean=sum(signal)/len(signal)

d. Rms value

While mean value can be null, we would like to be able to describe the amplitude of the signal. Rms value is one way to do it :

rms(signal)=\sqrt{\frac{1}{N}\sum_{t=1}^{N}(signal(t))^{2}}

 

Python
1
rms=np.sqrt(np.dot(signal,signal)/len(signal))

e. Energy of a signal

Depends on the amplitude and the length (number of points) of the signal.

E(signal)=\sum_{t=1}^{N}(signal(t))^{2}

 

Python
1
energy=np.dot(signal,signal)

 

f. Power of a signal

Square of the rms value.

P(signal)=\frac{1}{N}\sum_{t=1}^{N}(signal(t))^{2}

 

Python
1
power=energy/len(signal)

 

g. Euclidean distance between 2 signals

2 signals with the same dimension represented in the same space can be compared using the euclidean distance. This value is difficult to interpret, but is often used to compare it to another euclidean distance. It’s a good tool to evaluate the performance of our models and compare them.

d=\sqrt{\sum_{t=1}^{N}(signal_{1}(t)-signal_{2}(t))^{2}}

 

Python
1
euclidean=np.sqrt(sum((signal1-signal2)**2))

 

h. decomposition and recomposition of a signal (projection on a basis)

A signal can be decomposed on an orthonormal basis. Let’s build an orthogonal basis made of several sinus signals.

 

Resampling

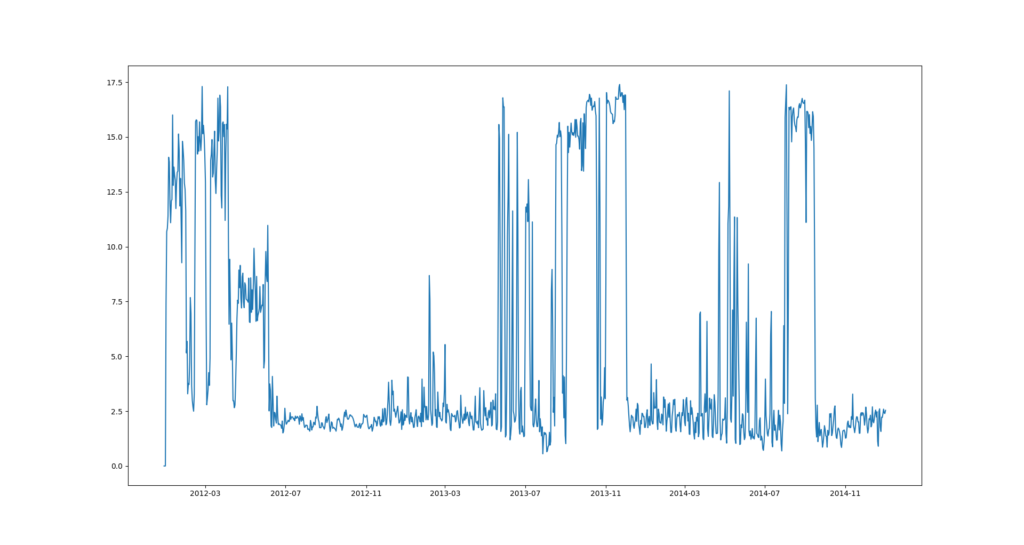
It’s unlikely that our time serie is distributed evenly with constant gap between 2 following points. Resampling techniques allows to decrease or increase the number of time steps in the serie and more important to make it with a regular distribution. Different rules can apply to calculate the missing values (mean, max, min, etc…).

Let’s resample our data to daily

Python
1
2
3
4
5
6
7
client1=client1.set_index('timestamp')
#resampling
client1_daily=client1.resample('D').mean()
 
#ploting values
plt.plot(client1_daily)
plt.show()

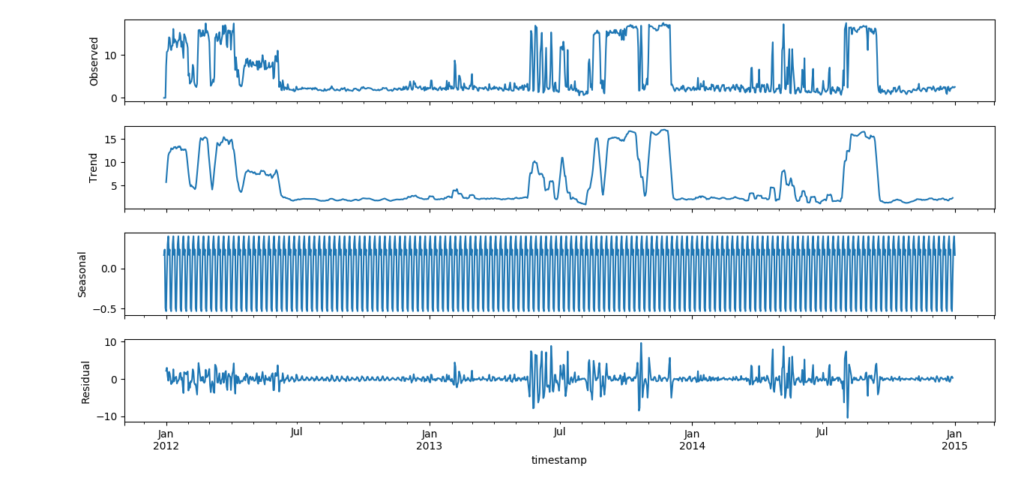
additive or multiplicative model?

Observed signals can be decomposed in 3 components : trend signal, seasonality signal, and noise signal.

Python
1
2
3
4
5
6
7
8
9
10
11
from statsmodels.tsa.seasonal import seasonal_decompose
 
result = seasonal_decompose(series, model='additive')
 
print(result.trend)
print(result.seasonal)
print(result.resid)
print(result.observed)
 
result.plot()
plt.show()

 

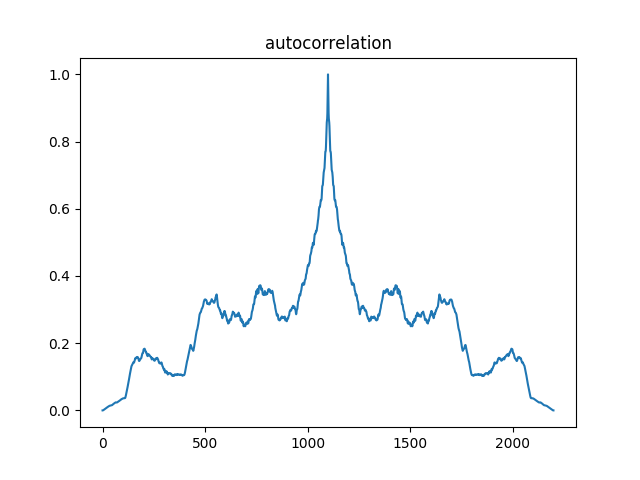
autocorrelation

Python
1
2
#autocorrelation
acr=autocorrelate(client1_flat)

Frequency domain

a. Change of basis. Fourier basis (f1 to fn)

Construction of the basis

ei2pift=cos(2pift)+jsin(2pift)

 

b. Signal decomposition in Fourier basis

Transformation of a signal u in the Fourier basis is given by the scalar product of u with the conjugate complex of each vector from the Fourier basis.

TF[u]_{n}=\sum_{0}^{N-1}u_{k}e^{-j2\pi\frac{n}{N}k}

Fourier transform is a complex number.

c. Spectrogram

Spectrum is the module of the Fourier transform

N : length of our signal

We begin by building the Fourier basis Fn, composed of N vectors. We then check that our basis is “almost” an orthogonal basis by calculating the dot product value of vectors 2 by 2 and comparing it to a threshold value.

Finally, decomposition of the signal u is given by the dot product of u with the conjugate of Fn vectors.

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
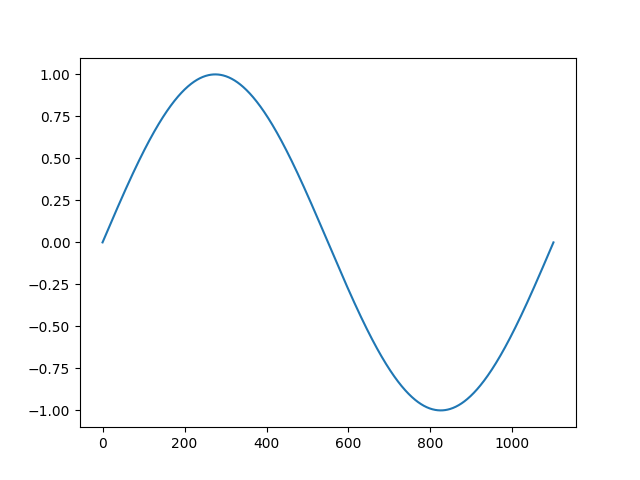
#Fourier transform of a 1d signal
import numpy as np
import math
import matplotlib.pyplot as plt
 
x=np.arange(0,300)
u=np.sin(x)*x+np.cos(x*2)
plt.plot(x,u)
plt.show()
 
#let u be our signal
 
N=len(u)
k=np.arange(0,N)
Fn=[]
freq=[]
 
#Fourier basis
for n in range(0,N):
f=np.exp(1j*2*math.pi*n/N*k)
Fn.append(f)
freq.append(n/N)
 
print(len(Fn))
print(len(freq))
 
#check orthogonality of the fourier basis
for f in range(len(Fn)):
other=[x for i,x in enumerate(Fn) if i!=f]
for l in range(len(other)):
dot=np.dot(Fn[f],other[l])
if dot>0.000001: #checking if the scalar is small
print(l,"th and",f,"th vectors are not orthogonal")
print("scalar product value is",dot)
print("False")
 
TF=[]
#decomposition in Fourier basis
for f in range(len(Fn)):
tfu=np.dot(u,Fn[f].conjugate())
TF.append(tfu/N)
 
#ploting of the spectrum
module=np.absolute(TF)
plt.plot(freq,module,'--o',ms=3)
 
 
#comparison with built in function
plt.plot(freq,abs(np.fft.fft(u))/N)
plt.show()

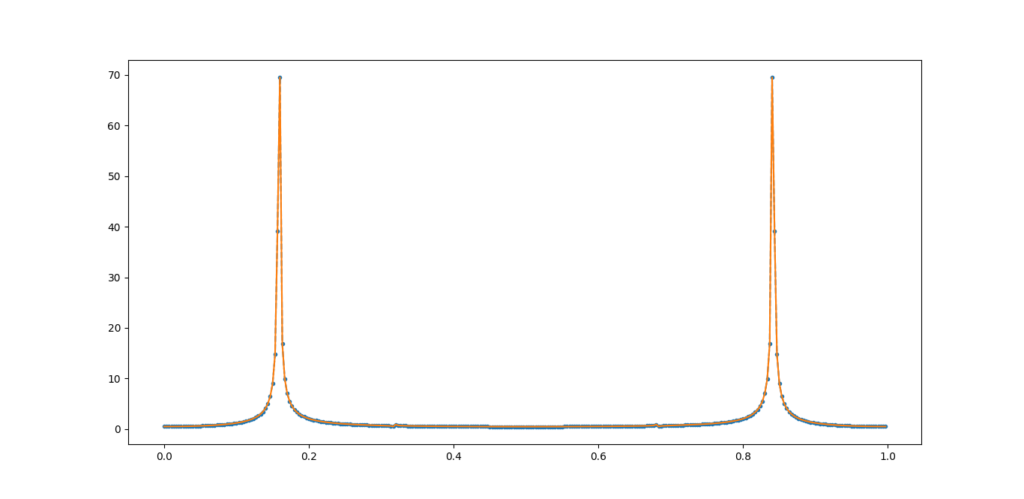
in blue, our Fourier function, in orange the one included in numpy. We can see that the values are matching, which validate our algorithm.

d. Convolution of 2 signals

Convolution is an operation which transform 2 signals (u1,u2) into an output signal (s) such as :

s(t)=\int_{-\infty }^{+\infty }u_{1}(\tau )u_{2}(t-\tau)d\tau

We often write convolution as follow :

s = u1 * u2 = u2 * u1

e. smoothing signal with convolution

Let’s define a noisy signal as follow.

Python
1
2
3
4
x=np.arange(0,300)
y=np.sin(x/6)+np.random.randn(300)/6
plt.plot(x,y)
plt.show()

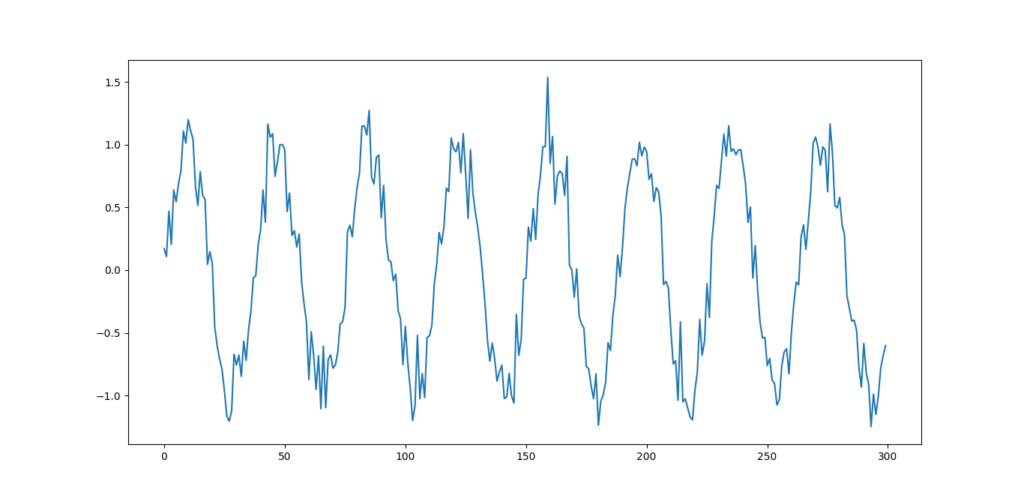
We want to use convolution to smooth the signal. Let’s start by averaging the signal with a small window.

u_{m}(t)=\frac{1}{T} \int_{-T/2}^{T/2}u(t-\tau)d\tau

We can write this equation as a convolution of the signal u with a gate signal such as :

gate=\frac{1}{T}\prod (t/T)

Forecasting series with LSTM

LSTM networks can be usde to predict the next output of a serie given the previous inputs. In the following, I am just going to describe a simple implementation of such a model.

We are going to predict a sinus signal with a trend defined as follow :

Python
1
2
3
4
5
6
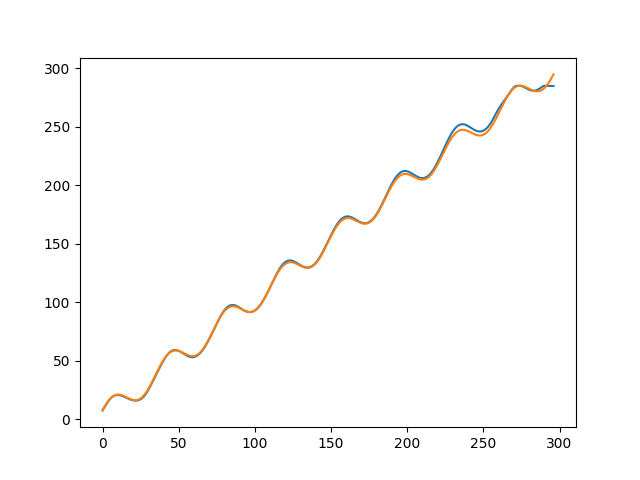
#data
x=np.arange(0,300)
y=10*np.sin(x/6)+x
 
plt.plot(x,y)
plt.show()

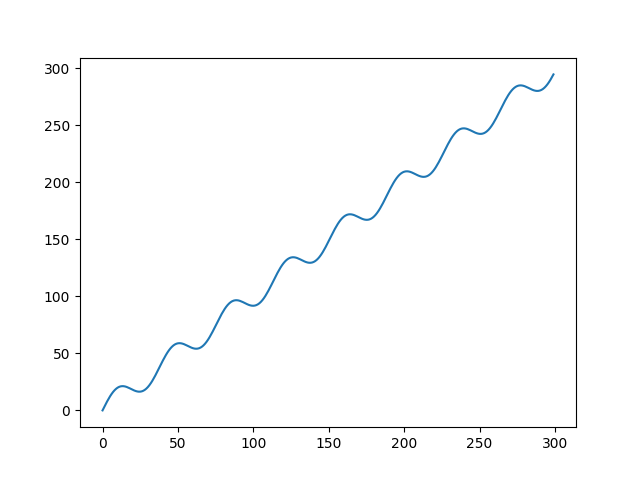
Given a number of previous time steps, we would like to predict the output of the signal. We need to define some parameters and to prepare the data so it could be fed properly into an LSTM keras layer.

Our signal contains len(x)=300 inputs points. Given the previous 10 points, we are going to predict the value of the next point.

Python
1
2
3
4
5
#parameters
input_size=len(x)
print("There are",input_size,"entries in our serie")
time_steps=10
batch_size=200

 

Preparation of the data.

The network will be fed with 10 inputs (time_steps) and 1 output. For each window of ten values in our serie we are going to send to the network a vector containing the values of the window (inputs) and the following value just after our window (ouput or label).

Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#data prepatation for neural network
inputs=[]
labels=[]
time_steps=3
for i in range(0,input_size-time_steps,1):
X_buffer=y[i:i+time_steps]
y_buffer=y[i+time_steps]
inputs.append(X_buffer)
labels.append(y_buffer)
inputs=np.asarray(inputs)
labels=np.asarray(labels)
 
 
print("inputs has shape",inputs.shape)
print("labels has shape",labels.shape)
 
inputs=np.reshape(inputs,(inputs.shape[0],1,inputs.shape[1]))

Now that pairs of inputs and label are ready, we can feed it into the network.

Building and training the model in Keras.

I choose a LSTM network with one hidden layer of 50 neurons.

Python
1
2
3
4
5
6
7
8
#building the network
model=Sequential()
model.add(LSTM(50,input_shape=(inputs.shape[1],inputs.shape[2])))
model.add(Dense(1))
model.compile(loss="mae",optimizer="adam")
 
#training
history=model.fit(inputs,labels,epochs=15000,batch_size=batch_size,verbose=1,shuffle=False)

 

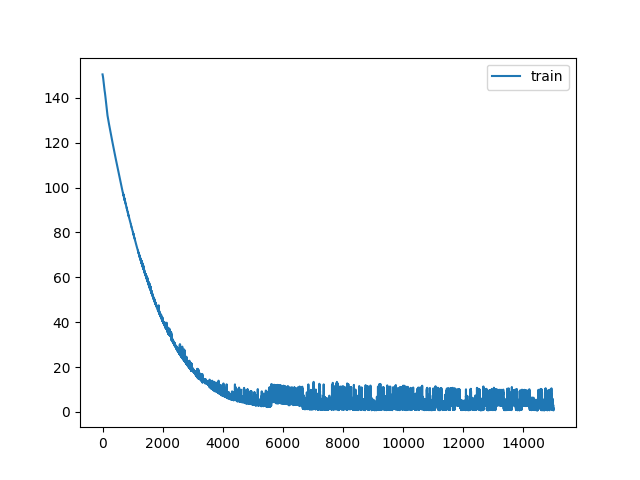
Plot the loss on the training set.

Loss on training set has a nice decreasing curve. Our network is learning properly.

Python
1
2
3
4
#visualization of the results
plt.plot(history.history['loss'],label='train')
plt.legend()
plt.show()

Make the prediction.

Python
1
2
3
4
5
#predictions
Ypred=model.predict(inputs)
plt.plot(Ypred)
plt.plot(labels)
plt.show()